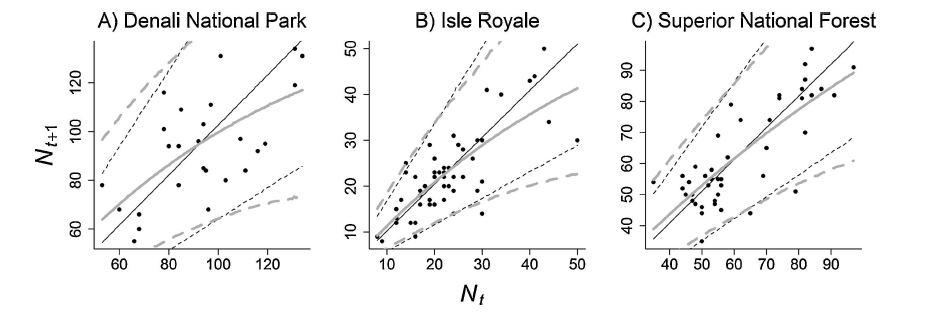
Figure 4 from Mech and Fieberg (2015)
My early research, largely in collaboration with Steve Ellner (Cornell University), was concerned with methods for performing population viability analysis, and in particular, methods for characterizing uncertainty in model projections [1,3-4,6]. This work led to the N = (5-10)T rule: in order to reliably estimate a non-zero extinction probability T years in to the future, one should have N = (5-10)T observations [1]. Although simple PVA models can often be constructed so as to have minimal bias, we've argued that poor precision often limits the utility of absolute predictions from these models [3]. Relative predictions are often more reliable; yet researchers should still quantify uncertainty when making relative comparisons [4]. We have explored different methods of estimating long-term population growth rates from stochastic matrix models, and also the potential for improving the precision of population forecasts by using experimental data that link environmental variability to estimates of vital rates [2]. We've reviewed various sensitivity indices and illustrated how they can be used to quantifying the impact of uncertainty on population forecasts [4,5].
1. Fieberg, J. and S.P. Ellner. 2000. When is it meaningful to estimate an extinction probability? Ecology, 81:2040-2047.
2. Fieberg, J. and S. P. Ellner. 2001. Stochastic matrix models for conservation and management: a comparative review of methods. Ecology Letters, 4: 244-266.
3. Ellner, S.P., J. Fieberg, D. Ludwig, and C. Wilcox. 2002. Precision of population viability analysis. Conservation Biology, 16:258-261.
4. Ellner, S.P. and J. Fieberg. 2003. Using PVA for management in light of uncertainty: effects of habitat, hatcheries, and harvest. Ecology 84:1359-1369.
5. Fieberg, J. and K. Jenkins. 2005. Assessing uncertainty in ecological systems using global sensitivity analysis: a case example of simulated wolf reintroduction effects on elk. Ecological Modeling, 187:259-280.
6. Fieberg, J. and D. F. Staples. 2006. The role of variability and uncertainty in testing hypotheses involving parameters in stochastic demographic models. Canadian Journal of Zoology 84:1698-1701.
7. Mech, D. and J. Fieberg. 2015. Growth Rates and Variances of Unexploited Wolf Populations in Dynamic Equilibria. Wildlife Society Bulletin 39: 41–48. doi: 10.1002/wsb.511.